Lamb(兰姆)波是二维波,与三维体波相比具有衰减速度慢,传播距离远的特点,因此常被用于大型板材的长距离及快速无损检测中。板材中兰姆波与管中、变截面波导介质中的导波一样,具有频散性与多模态性。加上环境噪声等多方面因素的影响,导波检测时传感器接收到的Lamb波信号非常复杂,属于非平稳随机信号,需要利用有效的信号处理技术提取有用的信息成分才能确定合适的激励方式,获得更好的检测成像效果。传统的处理Lamb波信号的方法包括反射系数法、傅里叶变换法、小波变换法、动态光弹法等,但是这些方法都有各自的不足。反射系数法是通过测量漏兰姆波的频散曲线来确定材料的性质,但测量难度较大。傅里叶变换只能处理线性非平稳的信号。小波变换法虽然在理论上能处理非线性非平稳信号,但是同傅里叶变换、短时傅里叶变换法一样,都受Heisenberg测不准原理制约,即时间窗口与频率窗口的乘积为一个常数,这就意味着如果要提高时间精度就得牺牲频率精度,反之亦然。当兰姆波中不同模态的频率比较接近时,不适用小波变换处理信号。动态光弹法能从Lamb波的应力分布观察到传播和频散,但是在实际检测中对硬件要求较高。
HilbertGHuang变换(HHT)是一种近几年发展起来的一种自适应信号处理方法,不受Heisenberg测不准原理制约,可以在时间和频率上同时达到很高的精度,非常适用于分析突变信号。笔者以薄壁铝板为研究对象,利用双重时间尺度的方法,即采用二维傅里叶变换法整体传播时间尺度,HilbertGHuang变换从单一信号时间尺度,将二者相结合对在铝板中不同位置采集到的Lamb波信号作数据处理与分析,与半解析有限元法得到兰姆波的频散曲线相对照,进而识别与分析铝板中兰姆波模态,获得较高的时间分辨率。
薄板中超声导波分离模态信号分析方法
一、传播特性的半解析有限元分析
在边界自由的固体板中,板材厚度与激励声波波长数量级相当时,在板中产生的应力波就是Lamb波.根据薄板两表面质点振动相位关系,Lamb波分为对称型Lamb波和反对称型Lamb波,分别用Sn、An 表示,n 为模态的阶次(n=0,1,2,3)。对称模态和反对称模态示意如图1所示,对称模态中沿着板厚方向中心点对称的各节点在厚度方向的位移方向相反;而反对称模态中,沿着板厚方向中心点对称的各节点在厚度方向的位移方向相同。
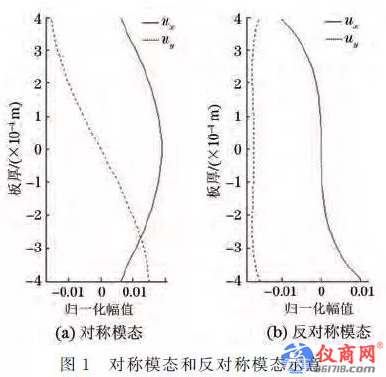
以铝板中Lamb波的传播为例,其频散曲线可采用半解析有限元法求得,只需要在波导介质的截面上作有限元离散,而沿波导介质传播方向的位移则以简谐波的振动方式表示,在对介质截面进行有限元离散后,根据哈密顿原理可以推导出导波在介质中的波动方程,求解特征值可以得到波数和频率的关系,进而绘制出频散曲线。
通过半解析有限元法,以铝板厚度d=0.8mm绘制铝板中导波的相速度和群速度频散曲线,得到的模态分布分别如图2,3所示。
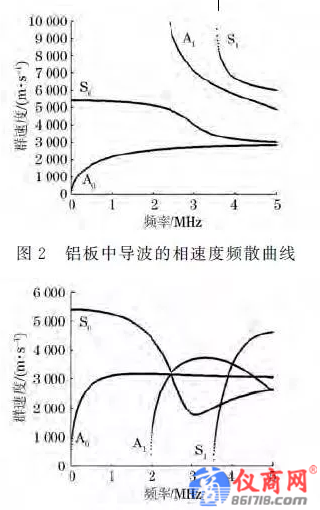
二、二维傅里叶变换
Lamb波在时间和空间上都可以通过二维傅里叶变换转换为二维各个离散频率点的频率G波数能量谱,从而分解出单个Lamb波,并可对其幅值进行测量。单个波动组分在时间上的频度称为频率,而在空间(距离)上的频度称为波数.由频率波数谱中某个波动组分的频率和波数,可以确定周期和波长。通过对接收信号的二维傅里叶变换,与理论计算得到的波数G频率的频散曲线进行对比,从而确定检测信号中包含的Lamb波模态。
三、HilbertGHuang变换
HilbertGHuang变换是由美国宇航局的Huang等于1998年在经典的Hilbert变换的基础上提出的.HilbertGHuang变换是一种自适应的信号处理方法,适用于分析非线性非平稳信号,其最大的特点是通过信号的EMD(经验模态分解),使非平稳信号平稳化,从而使瞬时频率有意义,进而导出有意义的希尔伯特时频谱.该方法由EMD与Hilbert谱分析两部分组成.EMD特别适合处理非线性、非平稳信号,可以把复杂的信号分解为一组按频率高低排列的固有模态函数(Intrinsic ModeFunction,IMF)之和,每一个IMF所包含的频率成分不仅与采样频率有关,还随信号变化而变化,因而EMD是一种自适应的信号处理方法。
1、EMD分解
EMD方法是通过特征时间尺度获得本征模函数,然后用有限个固有振动模态来分解时间序列数据.在EMD分解过程中,信号中最高频的成分先提取出来,所以第1个IMF分量是从检测信号中分离出的最高频成分,依次下去各阶IMF的频率逐渐降低,最后的余项代表了整个时间信号的趋势.因此原始信号可以表示为所有固有模态分量叠加之和加上余项,即:
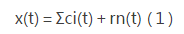
2、HHT谱分析
对式(1)分离的IMF进行希尔伯特变换,可把时间、频率、幅值画在三维图上,简称为HHT 谱,记为:
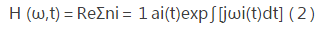
汇总所有IMF分量的HHT谱就得到了原始非平稳信号的Hilbert谱.按照这种方法得到Hilbert谱在联合的时间G频域中描述非平稳信号,具有非常高的时频分辨率。
基于EMD方法分解得到的各个IMF 分量具备实际的物理意义,可以表示信号内部从高频至低频的不同部分.同时,根据Hilbert谱中的时间幅值分布,可以转化为对能量进行有效表征的功率谱或能量谱。
试验方法
试验所用铝板密度为2700kg/m³,厚度d=0.8mm,平铺在绝缘工作台上.铝板中纵波速度为6370m/s,横波速度为3160m/s。铝板下方减震处理,超声探头位于其上方同侧.采用JSR公司DPR300超声波脉冲发射/接收器提供高压激励信号,脉冲振幅313V、能量3.91×10-5J、阻抗333Ω.接入中心频率f=1.0 MHz的高压激励直探头,直径1mm的水听器探头作为接收端.激发信号接入数字存储示波器(RIGOLDS1074B)触发通道,同步信号经过输出端接入示波器通道1,从而实现波形数字化,试验装置如图4所示。
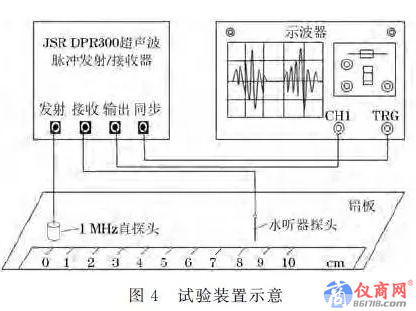
采用少量水作为耦合剂,DPR300 超声波发射/接收器发出的脉冲激励发射探头向铝板中发射纵波超声波,并同步触发数字示波器,水听器探头接收的是经传播后产生的超声Lamb波信号.在数字示波器上对显示的信号进行观察,通过旋转微调发射探头,可以获得显示幅值最高的信号,示波器对信号进行16次采样再取平均以提高信噪比.为了减小随机噪声对试验结果的影响,探头以1mm 的步长变化进行多次采样,以便根据笔者所用方法进行后续分析和处理。
试验结果及分析
1、二维傅里叶变换模态分析
将接收传感器先放在距离发射探头140 mm处,再使接收传感器以1mm 步长靠近发射探头,总采样组数为140组,得到包含时间和空间信息的兰姆波信号.铝板中Lamb波信号的时域图如图5所示,数字示波器的采样频率为10MHz,采样点数为600。
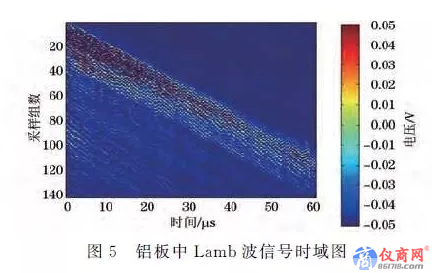
从图5中可以看到,在铝板中随着时间传播的兰姆波的整体状态.对所得信号做二维傅里叶变换,得到波数G频率关系,如图6(a)所示。
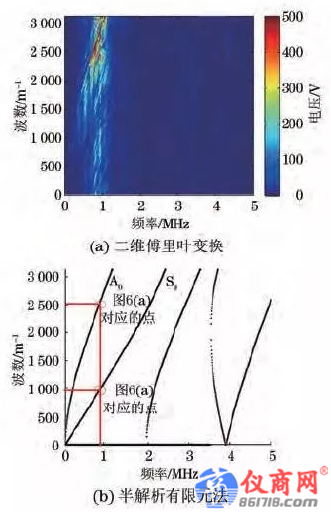
从图6(a)可以看出,铝板中传播模态的频率为0.98MHz,对应的波数为2500m-1及990m-1,因此在半解析有限元法绘制的波数G频率关系中可以找到与该频率、波数值对应的点位于A0 模态和S0模态上,并从图6(a)中可以看到A0 模态占据了主要能量.因此,通过这种方法在Lamb波整体的传播时间尺度上可以确定分离的模态及其能量大小.图7 兰姆波原始信号时域波形。
2、HilbertGHuang变换模态分析
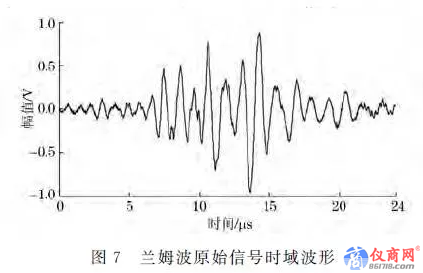
选用1MHz直探头发射Lamb波,距离换能器中心L=55mm 处以水听器探头作为接收端,示波器信号采样时间24μs,采集到的0.8mm 厚铝板内Lamb波时域波形如图7所示,横轴为时间,纵轴为幅值,以电压表示,根据图5中采样信息可知,在这一位置始波信号并未发生明显的能量衰减.然而时间轴上的信息则非常复杂,一方面Lamb波主要模态波的波包混叠在一起,体现了其固有的频散性和多模态特性;另一方面原始信号虽然经过示波器的16次采样取平均,但是噪声的频带比较宽且存在于整个时间段.因此原始时域波形上各模态峰值并不明显,难以准确提取获得有效的分析数据.对原始信号做EMD分解,前4阶IMF分量如图8所示.对照频谱图可以看出:
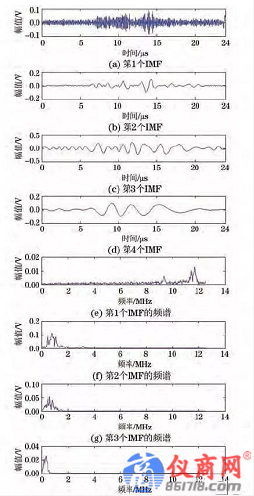
(1)低阶的IMF 包含了主要信息,从第4阶IMF开始能量非常微弱,与探头的中心频率也相差很远,为低频干扰信号,可以滤除而不会造成主要信息丢失。
(2)1阶IMF为信号中的高频成分,这其中除了信号本身混叠的高频分量外,主要为前文所述的环境噪声。
(3)2阶IMF和3阶IMF含有绝大部分能量,与原始信号的相关性也最好。
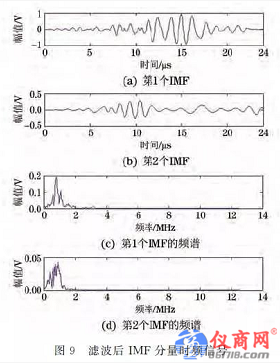
对不同模拟信号以及试验中采集的其他数据进行研究,可以获得各阶IMF信号变化规律.当原始信号为较清晰的低噪声信号时,EMD分解后的低阶IMF为主要信息成分,高阶为其他噪声;当原始信号有较多的环境噪声时,低阶IMF往往先是高频噪声,再高阶为其他噪声,滤波后IMF时频信号如图9所示.直接对多模态的Lamb波进行HHT变换易受高频噪声影响,分析的结果杂乱[9].因此,对于(2)中所述情况,为了不丢失信息,经过各种去噪方法,采用带通滤波技术对原信号进行处理之后再进行EMD分解即可滤除高频环境噪声。
重新分解经过处理后的信号,1阶、2阶IMF分量即为信号的主要成分,如图9所示,在中心频率1MHz附近有两个波包,需要利用重构算法获得具有较高信噪比的原始信号[10].因此,对其进行重构,经过希尔伯特变换后,根据幅值(能量)可以做出能量包络[11],如图10所示.以包络的峰值时刻作为信号到达的时间点,从图中可以更直接地读出S0 模态和A0 模态的波到达时刻.根据图2中厚度为0.8mm 铝板,1MHz中心频率所对应的A0 模态群速度为vA0 =3244m/s,S0 模态群速度为vS0=5297m/s,由L=55mm 可以计算得出A0 模态到达的理论时刻为16.5μs,S0 模态到达的理论时刻为10.1μs,两个模态的波形到达的时间差Δt=6.4μs.实际测量A0 模态到达的时刻为16.1μs,S0 模态到达的时刻为9.9μs,时间差Δt=6.2μs.理论数据和实际测量结果基本吻合,说明通过这种方法可以从单一信号时间尺度内准确区分各模态波的到达时间。
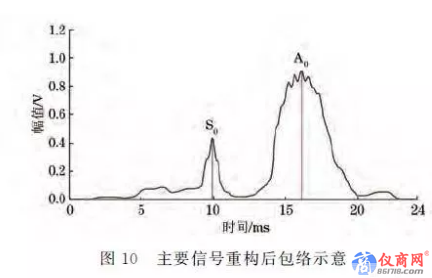
超声波在板状介质中传播存在多种模态,为了提高检测的速度与精度,在图像处理中对获取的检测信号进行模态分析是非常必要的.二维傅里叶变换可以从Lamb波整体的传播时间尺度上,根据一系列试验数据定性判定模态及其能量分布;HilbertGHuang变换则可以判定单一时间尺度信号内部不同频率特征的部分,经过合理的分解滤波重构,对有用IMF进行谱分析的方法可以将信号内不同模态进行定量区分.将这两种不同时间尺度分析方法结合半解析有限元法的理论数据进行验证,为超声导波用于薄板或复杂截面结构的无损检测提供一种可行的信号分析方法。




















